An autonomous surface vehicle (ASV) can reduce the number of sailing accidents caused by human error. In addition, onboard crew expenses are greatly reduced. The collision avoidance (CA) algorithm, as one key part of an autonomous ship, however, is always an intractable problem in terms of real-time, robustness, and rule compliance. How to deal with the massive uncertainties and complexity of the dynamic environment for local CA is still a challenge for researchers. Furthermore, compliance with the International Regulations for Preventing Collisions at Sea (COLREGS) has accentuated the calculation complexity of CA algorithms. In this blog, we introduce several popular methods of maritime collision avoidance.
There is no doubt that the artificial intelligence (AI) based method is one of the most popular ways for autonomous systems now. Benefiting from the development and applications of Machine Learning (ML) and Deep Learning (DL) in the automotive industry, many researchers are trying to apply it to the maritime CA context. By learning from labeled data sets, a neural network (NN) based model is trained and then used for the target scenarios. Such models, with multiple hidden layers in a neural network, can directly map the input from the perception environment data to the specified output, e.g., control commands or desired new route. This method usually skips the data processing and model design of intermediate steps, which is also called end-to-end learning. So far, some research results have shown the effectiveness of the DL in maritime CA [1, 2]. However, low interpretability of the trained model is still a common problem, which makes it difficult to be accepted in the industry. Besides, the processing of sensors and uncertainties is included in the end-to-end DL, which is similar but still varies concerning the other methods. The lack of a standardized description of the perceived maritime environment also leads to differences between the data sets, which reduces the reliability of the data.
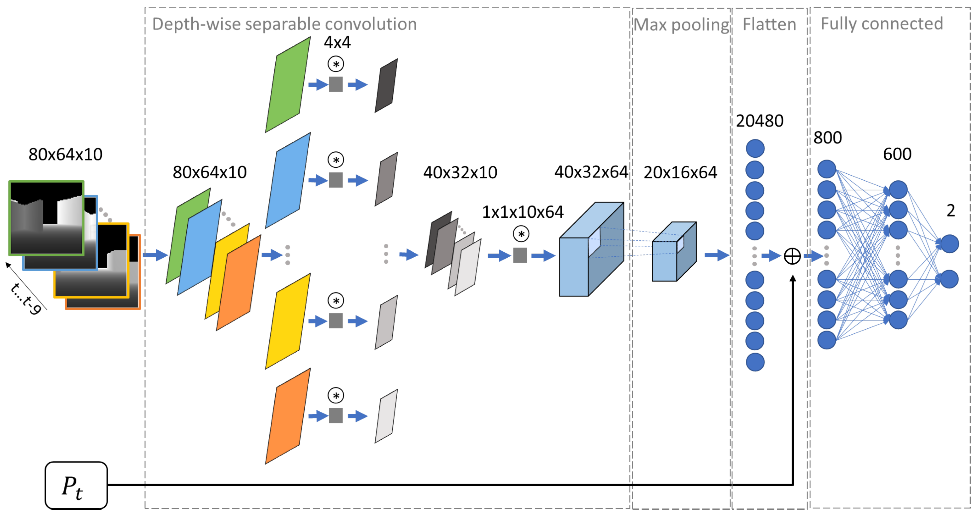
Figure 1: Architecture of the one convolutional neural network [3].
Fuzzy logic is a popular method, which essentially is a form of many-valued logic. For instance, the distance between one target and the own ship can be modeled as a value between 0 and 1. With the pre-set thresholds, a decision can be made to keep a safe distance with other ships. The advantage is that it can easily combine expert knowledge or rules like COLREGs. However, the dependence on prior knowledge is always a critical issue for this method.
Another option is field method, such as the artificial potential field (APF) and the Limited Cycle Method (LCM). A potential field is created to describe the collision risk with objects and then converts the path-finding problem into a gradient-descent problem or a dynamic-model-solving problem. For example, Lyu and Yin (2019) used this modified APF for ASVs in real-time path planning [4]. However, the main drawback of the field method is that the algorithm might be trapped in a local minimum, especially in terms of the dynamic factors.
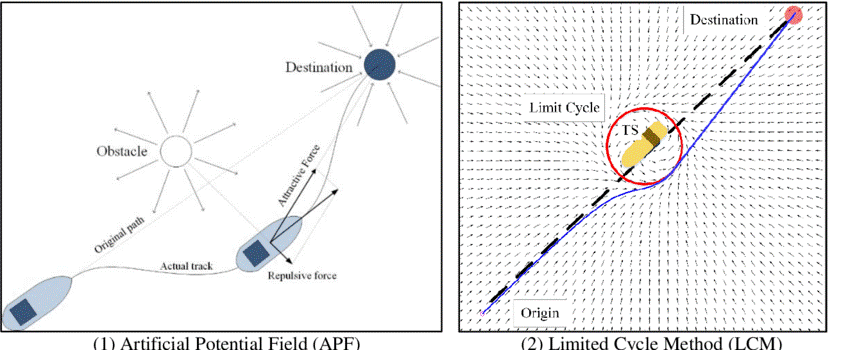
Figure 2: Potential Fields Methods [5].
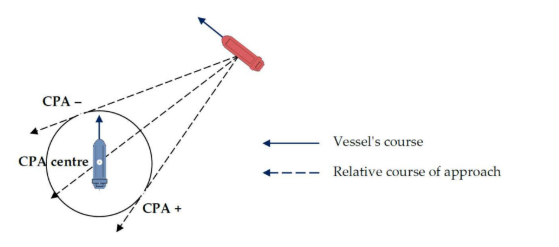
Figure 3: One example of Fuzzy logic.
Graph search methods, a kind of computational algorithm for the optimization problem, are classical methods for path finding and collision avoidance. The well-known algorithms, like, A* and their numerous variants, have been validated in various fields. These methods search the path directly on the graph space or map. One variant, Theta*, was used and extended by Singh et al. (2018) in an environment cluttered with static and moving obstacles and different current intensities [6]. The variant, Hybrid A*, unlike conventional variants that only allow visiting centers, corners or edges of grid cells, associates with each cell a continuous state of vehicles (Dolgov et al., 2008) [7]. Ship dynamics can be considered during the graph search. However, there is still a common problem with these methods that the computational load depends on the resolution of the map or the sample number, even though there have been a lot of work to overcome it.
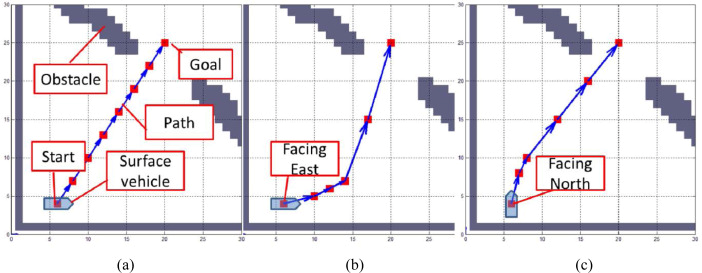
Figure 4: One example of A* method for maritime collision avoidance [8].
Optimization-problem solving can also be a class of solutions for collision avoidance. These methods try to find the corresponding variables to optimize the cost function with all kinds of constraints. Typically, such optimization problems can be solved with computational algorithms, such as the evolution algorithm (EA) or the ant-colony optimization (ACO) algorithm. However, these methods usually require a relatively long computation time, especially when the ships are in complex scenarios. Apart from that, the optimal solution is usually given by solvers, which is not very transparent to users. EA might not converge within the desired time in complex scenarios, and a discrete algorithm’s computational time can be slow when the sample numbers or solution space are large. If we consider the system as a control system, then it becomes an optimal control problem. The solution can be found by some optimal control methods, e.g. model predictive control (MPC). But, for complex systems, it is difficult to construct and maintain optimal controllers, or non-trivial ways are needed for these systems, which also reduces the real-time performance.
Since each method has certain limitations, finding an all-purpose approach for all cases is almost impossible. Combining some methods can be a good idea. Of course, such hybrid methods are more complex to design and more tests are needed to prove their effectiveness.
References
[1] Cheng, Yin, and Weidong Zhang. “Concise deep reinforcement learning obstacle avoidance for underactuated unmanned marine vessels.” Neurocomputing 272 (2018): 63-73.[2] Meyer, Eivind, et al. “COLREG-compliant collision avoidance for unmanned surface vehicle using deep reinforcement learning.” IEEE Access 8 (2020): 165344-165364.
[3] Cimurs, Reinis, Jin Han Lee, and Il Hong Suh. “Goal-oriented obstacle avoidance with deep reinforcement learning in continuous action space.” Electronics 9.3 (2020): 411.
[4] Lyu, Hongguang, and Yong Yin. “COLREGS-constrained real-time path planning for autonomous ships using modified artificial potential fields.” The Journal of navigation 72.3 (2019): 588-608.
[5] Huang, Yamin, et al. “Ship collision avoidance methods: State-of-the-art.” Safety science 121 (2020): 451-473.
[6] Singh, Yogang, et al. “A constrained A* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents.” Ocean Engineering 169 (2018): 187-201.
[7] Dolgov, Dmitri, et al. “Practical search techniques in path planning for autonomous driving.” Ann Arbor 1001.48105 (2008): 18-80.
[8] Yang, Joe-Ming, Chien-Ming Tseng, and P. S. Tseng. “Path planning on satellite images for unmanned surface vehicles.” International Journal of Naval Architecture and Ocean Engineering 7.1 (2015): 87-99.
About the Author: Tianlei Miao
Tianlei has studied in Naval Architecture and Ocean Engineering at Zhejiang University, where he graduated with his bachelor’s degree in 2017. During his bachelor’s years, Tianlei was awarded several scholarships such as National Scholarship in China and has held different leadership positions, such as President of the Student Union of Ocean College at Zhejiang University. He also spent 6 months at the Technical University of Munich in Mechanical Engineering.
In 2017, Tianlei started a dual M.Sc in Maritime Engineering at both Norwegian University of Science and Technology (NTNU), Norway, and the Royal Institute of Technology (KTH), Sweden. As part of the master’s program, he focused on the generation of the full-envelope hydrodynamic database of hydrostatic AUVs under the supervision of Prof. Dr. Ivan Stenius and Prof.Dr. Marilena Greco.
