Neural Networks are state-of-the-art algorithms for image recognition and classification. In our new blog you can read how do these algorithms fit into safety-case scenarios where mistakes can lead to the loss of human life or to the serious damage to the environment.
Safety-critical systems are those systems whose failure could result in the death of people, damage to equipment/property and environmental harm [1]. Medical systems and autonomous vehicles as presented in Fig. 1., are safety-critical systems that rely on image recognition and classification for their correct and safe operation. Neural Networks are state-of-the-art algorithms for image recognition. NNs are machine learning (ML) algorithms modeled loosely on the human brain, trained using labeled training samples of the different image classes that are supposed to classify.
Some of the most important attributes that we have to achieve while dealing with classifiers in safety-critical systems with ML components are:
- Robustness – is the classifier prone to errors and how it behaves in case unknown or noisy inputs?
- Explainability – can we trace back decisions?
- Performance – does the classifier have high accuracy, precision and other relevant metrics?
Figure 1. Autonomous vehicle on a road [2]
While NNs indeed perform excellently on images that belong to the classes used in the training process referred to as in-distribution data (ID), unfortunately they often easily misinterpret images that do not belong to the trained classes, referred to as out-of-distribution data (OOD). The research shows that NNs tend to make high confidence predictions even for completely unrecognizable inputs [3].
If we take autonomous vehicles as a case-study, the traditional way to classify traffic signs is to train one multi-class NN. In the case the sign from new class appears, the problem is that this classifier is likely to give high confidence output stating that it belongs to one of the existing classes.
As the classifier can wrongly classify speed limits signs or stop signs, it is clear that such behavior is unacceptable if we want to have fully autonomous vehicles on our roads anytime in the future. From the previous example, it can be also concluded that the level of control over the input data is low. Therefore, classifiers need to be aware of new kinds of inputs [3],[4]. We want to design such classifiers that are behaving differently in the case of OOD or noisy data, so we already will be able to conclude that something is wrong with the input data. However, it is crucial to perform such a task without affecting the performance of the NN.
Unfortunately, in real-case scenarios, the level of control over the input data is low. That is why we are researching the approach to use one-class classifiers, as such algorithms are suitable for the training with the data that we are aware of, while everything else is considered as unknown. Such algorithms are trained only on the ‘normal’ data, which is in this case the data that belongs to the known classes. It learns the boundaries of known inputs and any input that lies outside the boundary is classified as an outlier. Some of the common one-class algorithms are:
- One-Class Support Vector Machine (OCSVM) [5];
- Isolation Forest (IF) [6],
- Local Outlier Factor (LOF) [7].
The OCSVM algorithm
This algorithm was first proposed by Schölkopf et. al. and in recent years, it has been widely used in various fields. The OCSVM is based on the traditional Support Vector Machine (SVM) algorithm but unlike the SVM, its aim is to solve classification problems that use only one type of samples. The SVM learns to distinguish between two classes in a training dataset, by fitting a hyperplane that optimally divides both classes. OCSVM is using a similar concept to the SVM, but instead of a hyperplane used to separate two classes, it constructs the optimal hypersphere to encompass all of the instances. Every sample that is calculated outside the hypersphere is marked as unknown [5].
The IF algorithm
This algorithm differs from many other Anomaly Detection (AD) algorithms in a way that it tries to detect anomalies rather than profiling normal model behavior. This is a tree-based AD algorithm. It is based on the idea that anomaly points are much easier to isolate than the normal data points. This algorithm generates partitions of the dataset by randomly selecting a feature and then randomly selecting a split value for that feature. It presumes that anomalies will have less random partitions compared to normal points [6].
The LOF algorithm
LOF algorithm provides a score that tells how likely a certain data point is an outlier/anomaly. It is a density-based algorithm for unsupervised outlier detection, based on k-nearest neighbors. This algorithm tries to find anomalous data points by measuring the local deviation of a given data point with respect to its neighbors. The algorithm is based on the idea that the density around an anomaly point is significantly different from the density around its neighbors. It uses the relative density of a sample against its neighbors to calculate the degree of the object being marked as an anomaly. One of the issues of the LOF is scalability as the computations are memory-intensive. Another disadvantage is that the user has to set the “k” value [7].
Proposed architecture
One of the ways to make the classification module more robust is to design a classifier architecture in such a way that in the case of OOD data, a lower probability is given to all output classes. Such architecture should provide the ability of the OOD data detection by simply setting a threshold-based detection algorithm, while also enabling us to understand the model behaviour more. One of the approaches we work currently is instead of a multi-class network to train multiple one-class classifiers on certain features and combine them in one model. This is presented in Figure 2. More information will become available, through a paper, in the future.
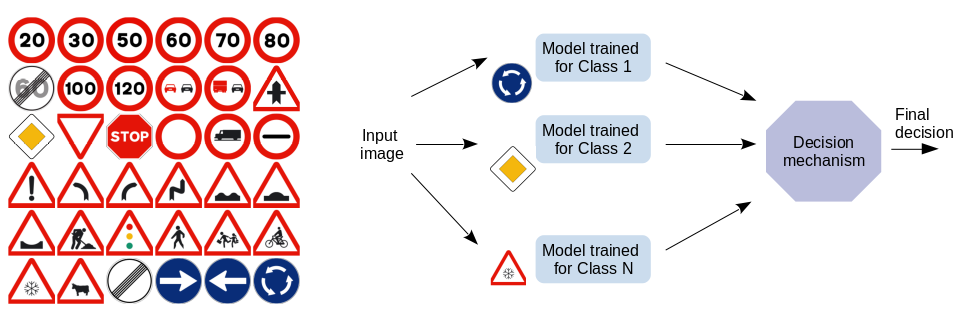
Figure 2. Ensemble of one-class classifiers for multi-class classification.
References
[1] Sommerville, Ian (2015). Software Engineering (PDF). Pearson India. ISBN 978-9332582699.[2] Image source – online: https://indianconventions.com/acoustic-vehicle-alerting-system-market-analysis-trends-growth-size-share-and-forecast-2019-to-2025-2/ [Accessed] September 2021
[3] S. Liang, Y. Li, and R. Srikant, “Enhancing The Reliability of Out-of-distribution Image Detection in Neural Networks,” 2018
[4] D. Ugrenovic, J. Vankeirsbilck, D. Pissoort, T. Holvoet and J. Boydens, “Designing Out-ofdistribution Data Detection using Anomaly Detectors: Single Model vs. Ensemble,” XXIX International Scientific Conference Electronics (ET), Bulgaria, 2020
[5] B. Schölkopf, J. C. Platt, J. Shawe-Taylor, A. J. Smola and R. C. Williamson, “Estimating the Support of a High-Dimensional Distribution,” Neural Computation, vol. 13, no. 7, pp. 1443-1471, 2001.
[6] F. T. Liu, K. M. Ting and Z. Zhou, “Isolation Forest,” 2008 Eighth IEEE International Conference on Data Mining, Pisa, 2008, pp. 413-422
[7] M. M. Breunig, H. Kriegel, R.T. Ng and J. Sander. “LOF: Identifying Density-Based Local Outliers.” ACM SIGMOD, 2000.
Author: Dejana Ugrenovic (former ESR4)


