Parts of Speech (POS) tagging is a text processing technique to correctly understand the meaning of a text. POS tagging is the process of assigning the correct POS marker (noun, pronoun, adverb, etc.) to each word in an input text. We discuss POS tagging using Hidden Markov Models (HMMs) which are probabilistic sequence models.
Given a sequence (words, letters, sentences, etc.), HMMs compute a probability distribution over a sequence of labels and predict the best label sequence. POS tagging is an underlying method used in conversational systems to process natural language input. Conversational systems in a safety-critical domain such as healthcare have found to be error-prone in processing natural language. Some of these errors may cause the system to respond in an unsafe manner which might be harmful to the patients.
Part-of-Speech Tagging
Part-of-Speech (POS) (noun, verb, and preposition) can help in understanding the meaning of a text by identifying how different words are used in a sentence. POS can reveal a lot of information about neighbouring words and syntactic structure of a sentence. POS tagging is the process of assigning a POS marker (noun, verb, etc.) to each word in an input text. The input to a POS tagging algorithm is a sequence of tokenized words and a tag set (all possible POS tags) and the output is a sequence of tags, one per token. Words in the English language are ambiguous because they have multiple POS. For example, a book can be a verb (book a flight for me) or a noun (please give me this book). POS tagging aims to resolve those ambiguities.
There are various common tagsets for the English language that are used in labelling many corpora. 45-tag Penn Treebank tagset is one such important tagset [1]. This tagset also defines tags for special characters and punctuation apart from other POS tags. The Brown, WSJ, and Switchboard are the three most used tagged corpora for the English language. The Brown corpus consists of a million words of samples taken from 500 written texts in the United States in 1961. The WSJ corpus contains one million words published in the Wall Street Journal in 1989. The Switchboard corpus has twice as many words as Brown corpus. The source of these words is recorded phone conversations between 1990 and 1991. For tagging words from multiple languages, tagset from Nivre et al. [2] is used which is called the Universal POS tagset. This tagset is part of the Universal Dependencies project and contains 16 tags and various features to accommodate different languages. The main application of POS tagging is in sentence parsing, word disambiguation, sentiment analysis, question answering and Named Entity Recognition (NER).
Hidden Markov Models
The Hidden Markov Models (HMM) is a statistical model for modelling generative sequences characterized by an underlying process generating an observable sequence. HMMs have various applications such as in speech recognition, signal processing, and some low-level NLP tasks such as POS tagging, phrase chunking, and extracting information from documents. HMMs are also used in converting speech to text in speech recognition. HMMs are based on Markov chains. A Markov chain is a model that describes a sequence of potential events in which the probability of an event is dependant only on the state which is attained in the previous event. Markov model is based on a Markov assumption in predicting the probability of a sequence. If state variables are defined as ![]() a Markov assumption is defined as (1) [3]:
a Markov assumption is defined as (1) [3]:
(1) ![]()

Figure 1. A Markov chain with states and transitions
Figure 1 shows an example of a Markov chain for assigning a probability to a sequence of weather events. The states are represented by nodes in the graph while edges represent the transition between states with probabilities. A first-order HMM is based on two assumptions. One of them is Markov assumption, that is the probability of a state depends only on the previous state as described earlier, the other is the probability of an output observation ![]() depends only on the state that produced the observation
depends only on the state that produced the observation ![]() and not on any other states or observations (2) [3].
and not on any other states or observations (2) [3].
(2) ![]()
An HMM consists of two components, the A and the B probabilities. The A matrix contains the tag transition probabilities ![]() and B the emission probabilities
and B the emission probabilities ![]() where
where ![]() denotes the word and
denotes the word and ![]() denotes the tag. The transition probability, given a tag, how often is this tag is followed by the second tag in the corpus is calculated as (3):
denotes the tag. The transition probability, given a tag, how often is this tag is followed by the second tag in the corpus is calculated as (3):
(3) ![]()
The emission probability, given a tag, how likely it will be associated with a word is given by (4):
(4) ![]()
Figure 2 shows an example of the HMM model in POS tagging. For a given sequence of three words, “word1”, “word2”, and “word3”, the HMM model tries to decode their correct POS tag from “N”, “M”, and “V”. The A transition probabilities of a state to move from one state to another and B emission probabilities that how likely a word is either N, M, or V in the given example.
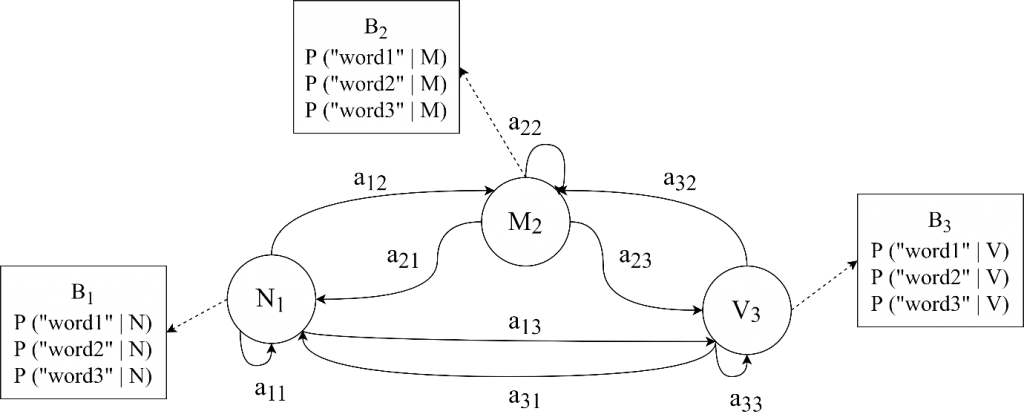
Figure 2. A Hidden Markov Model with A transition and B emission probabilities.
HMM Tagger
The process of determining hidden states to their corresponding sequence is known as decoding. More formally, given A, B probability matrices and a sequence of observations ![]() , the goal of an HMM tagger is to find a sequence of states
, the goal of an HMM tagger is to find a sequence of states ![]() . For POS tagging the task is to find a tag sequence
. For POS tagging the task is to find a tag sequence ![]() that maximizes the probability of a sequence of observations of
that maximizes the probability of a sequence of observations of ![]() words
words ![]() (5).
(5).
(5) ![]()
The Viterbi Algorithm
The decoding algorithm for the HMM model is the Viterbi Algorithm. The algorithm works as setting up a probability matrix with all observations ![]() in a single column and one row for each state
in a single column and one row for each state ![]() . A cell in the matrix
. A cell in the matrix ![]() represents the probability of being in state
represents the probability of being in state ![]() after first
after first ![]() observations and passing through the highest probability sequence given A and B probability matrices. Each cell value is computed by the following equation (6):
observations and passing through the highest probability sequence given A and B probability matrices. Each cell value is computed by the following equation (6):
(6) ![]()
Figure 3 shows an example of a Viterbi matrix with states (POS tags) and a sequence of words. A greyed state represents zero probability of word sequence from the B matrix of emission probabilities. Highlighted arrows show word sequence with correct tags having the highest probabilities through the hidden states.
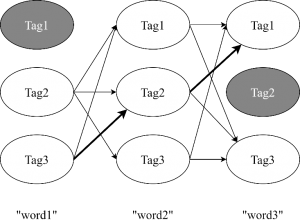
Figure 3. Viterbi matrix with possible tags for each word.
The Viterbi algorithm works recursively to compute each cell value. For a given state ![]() at time
at time ![]() , the Viterbi probability at time
, the Viterbi probability at time ![]() ,
, ![]() is calculated as (7):
is calculated as (7):
(7) ![]()
The components used to multiply to get the Viterbi probability are the previous Viterbi path probability from the previous time ![]() ,
, ![]() the transition probability from the previous state
the transition probability from the previous state ![]() to current state
to current state ![]() , and
, and ![]() the state observation likelihood of the observation symbol
the state observation likelihood of the observation symbol ![]() given the current state
given the current state ![]() .
.
Conclusion
n this blog, we discussed POS tagging, a text processing technique to extract the relationship between neighbouring words in a sentence. POS tagging resolves ambiguities for machines to understand natural language. In conversational systems, a large number of errors arise from natural language understanding (NLU) module. POS tagging is one technique to minimize those errors in conversational systems. These systems in safety-critical industries such as healthcare may have safety implications due to errors in understanding natural language and may cause harm to patients.
References
[1] M. MARCUS, B. SANTORINI, and M. MARCINKIEWICZ, “Building a Large Annotated Corpus of English: The Penn Treebank,” Comput. Linguist., 1993.[2] J. Nivre et al., “Universal dependencies v1: A multilingual treebank collection,” in Proceedings of the 10th International Conference on Language Resources and Evaluation, LREC 2016, 2016.
[3] M. J. H. Jurafsky, Daniel, “Speech and Language Processing 3rd Edition Draft.” [Online]. Available: https://web.stanford.edu/~jurafsky/slp3/.
About the Author: Haris Aftab
 Haris has recently completed his master’s degree in Computer and Information Security from South Korea in February 2019. His area of research was ensuring interoperability in IoT standards. Before that, he worked in the IT industry for about 5 years as a Software Engineer for the development of mobile applications of Android and iOS. His interest in technology, mobile devices, IoT, and AI having a background in Software Engineering brought him to work in this exciting domain.
Haris has recently completed his master’s degree in Computer and Information Security from South Korea in February 2019. His area of research was ensuring interoperability in IoT standards. Before that, he worked in the IT industry for about 5 years as a Software Engineer for the development of mobile applications of Android and iOS. His interest in technology, mobile devices, IoT, and AI having a background in Software Engineering brought him to work in this exciting domain.


