The use of machine learning (ML) algorithms is becoming common in safety-critical autonomous systems (AS) such as autonomous vehicles and advanced robotic tasks. These systems are nonlinear and interact with nonlinear (dynamic) environments, resulting in stochastic outcomes. In this post, we introduce how ML is applied to such dynamic systems, more specifically for the autonomous vehicles, and a first discussion on how its problems can have a nonlinear link between them.
Figure 1. Turbulence in the tip vortex from an airplane wing [source].
The use of machine learning (ML) algorithms is becoming common in safety-critical autonomous systems (AS) such as autonomous vehicles and advanced robotic tasks. These systems are nonlinear and they interact with dynamic environments, resulting in stochastic outcomes. In this post, we introduce how ML is applied to such dynamic systems, more specifically for autonomous vehicles, and introduce the discussion on how its problems can have a nonlinear link between them.
Linear Systems: a quick overview
Linear systems are understood as approximate models. They facilitate the understanding of complex problems and they also correctly capture the behaviors of certain domains such as finance and economics. It has some important and simple premises:
- Homogeneity: the output of a model is proportional to its input, that is, the scale does not matter since it is just necessary for inspecting a system in isolation and adding a scalar to it if one wants to predict or estimate outputs.
- Additivity: when adding two or more effects, it results in a combined outcome, that is, 1 engine + 1 engine = power of 2 engines. It means that we can also inspect the object or the system in isolation and make predictions or estimations based on the additive property.
Advantages: system properties can be analyzed in isolation. Linear models also tend to be simple and intuitive. Some real-life examples include, making predictions of social-economic behaviors, calculating medicine doses based on patients’ weights, etc.
Drawbacks: it does not focus on how actions affect the environment, that is, there is no feedback and thus, is generally static in time.
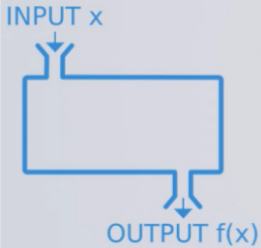
Figure 2. Proportionality in linear systems [source].
Figure 3. Synergies in nonlinear systems [source].
Nonlinear Systems: a quick overview
Nonlinear systems are the ones in which the change of the output is not proportional to the change of the input and cannot be solved by a linear equation. These systems are more complex and more common in real world scenarios.
Differently from linear models, additivity and homogeneity properties do not work as expected. That is, the relationship between two objects or systems cannot be explained by the mathematical relationship of proportionality.
Moreover, these objects when combined can result in a decrease in their properties (interference) or even produce exponential outcomes (synergy). Besides, nonlinear systems are not static in time. A property known as feedback loop. That is, there is an influence between two objects or systems through time, affecting their outcomes in both directions, positively or negatively. Despite the existence of linear time variant systems, nonlinear systems have no general analytical expression that gives a solution in a linear form. Sometimes linear time varying systems can be calculated as an approximation for nonlinear systems by linearizing along a solution trajectory, but once again, it is just an approximation.
These types of dynamic systems have a huge amount of stochastic behavior and are very sensitive to small changes in the initial conditions, leading to several different outcomes, a process known as the butterfly effect and studied by chaos theory practitioners.
Advantages: nonlinear systems comprehend the majority of real problems. It means that a solution that takes into account the nonlinearity of a problem is more prone to be accurate.
Drawbacks: such systems are stochastic, that is, they have (apparently) several randomnesses in the process. Besides, they are complex to model, develop, and evaluate.
The World is Nonlinear
Even though we humans make plans in a linear way, in fact, our lives and the environment that we interact with are nonlinear. A simple example of this nonlinearity could be the small decisions that we do in our lives and lead us to different paths (butterfly effect). I could enumerate many examples but below I show some of them:
- Society and music: Society influences the type of music that is produced in a determined period of time, and on the other hand, the music also influences the people in return, a constant feedback loop through time.
- Disease spread: it cannot be modeled by simply using the properties of homogeneity, as described by linear models, since in most infectious diseases the spreading speed of infection is modeled by exponential curves.
- Chemistry: certain chemical interactions do not produce more properties as a summing between them, but the opposite, what characterizes the non-additive phenomena. Moreover, combining two medical treatments can produce much more than a double of the effects in the patient, or even a single but totally unexpected effect.
- Social networks: these systems are extremely nonlinear and are usually modeled the same way as one could try to model the spreading of infectious disease, in fact, both can be studied by the theory of complex networks.
- Vehicles interacting with the environment: a complex system interacting in a dynamic environment will produce several unexpected outputs.
Could you mention another example?
How to Deal with Nonlinear Problems?
There are several ways to do it but it is with machine learning (ML), an Artificial intelligence (AI) sub-field, that the world is investing a lot of resources to deal with modern real world problems. The reason is that ML learns nonlinear patterns from data, being very useful for complex pattern recognition tasks for several types of objects such as audio, images, etc.
Artificial intelligence (AI) techniques usually try to mimic human/nature abilities while ML is an AI sub-field aiming at learning from data. Deep learning (DL), is a subfield of ML that applies mostly to neural networks on a large scale: a large number of parameters and layers (deep).
ML is very practical to use, and fast for deploying a minimally viable solution. Besides, ML does not need to have a model regarding the domain nor too much prior knowledge about the attributes.
Regarding DL, these tasks tend to be less daunting since there is almost no necessity of applying preprocessing in data in order to get reasonable answers. DL has at least four fundamental architectures: Unsupervised Pre-trained Networks; Convolutional Neural Networks; Recurrent Neural Networks; and Recursive Neural Networks. It is applied to several domains, including autonomous vehicles (AV).
DL is a strong and useful technology, however, it is not trustworthy for such critical and high nonlinear scenarios due to three main reasons:
- Design errors: ML model inaccuracies (“all models are wrong but some are useful”)
- Data incompleteness: insufficient test coverage and incomplete learning
- Environment oversimplification: unseen interactions, behaviors or problems
Thus, the aforementioned limitations bring important challenges for adopting DL for AV.
Challenge #1: 99% accuracy is not enough
Figure 4. Tesla Model X fatal crash [source].
Figure 5. Uber deadly crashes a cyclist [source].
Wrong decisions (even on a small percentage) can lead to catastrophes, that is, 1% of wrong decisions can be catastrophic (for people inside or outside the car). Beyond that, it is normal that a car needs to interact with unexpected objects and situations in the environment. In this blog, the author shows a lot of unexpected interactions that can lead the ML to make ambiguous decisions. For example, looking at Figure 6, could you know if there is a clock tower in front of the vehicle or is the vehicle in front of a tram? It is a difficult task for an ML algorithm. Moreover, facing similar objects that do not have the same objective such as in the second Figure can be a challenge for ML algorithms.
Figure 6. Mirror, mirror on the wall… [source].
Figure 7. AI for full self-driving [source].
Challenge #2: ML threats can mislead DNN decisions
There are at least 4 main problems that can happen with ML algorithms during operation time:
Distributional shift: data distribution changes while the ML model is online: Distributional differences between training data and data at runtime. Ex: Deteriorate traffic sign images, degraded perception, or other changes in the characteristics of the objects.
Figure 8. Deteriorate traffic sign image.
Anomalies: identification of an anomalous input or behavior. Some examples of anomalous images in an autonomous vehicle camera include a Fault in the Clock System (Figure 9) and Color Error due to an Image Pipeline Fault (Figure 10).
Figure 9. Evaluating Functional Safety in Automotive Image Sensors (1) [source].
Figure 10. Evaluating Functional Safety in Automotive Image Sensors (2) [source].
Adversarial examples: perturbations that lead to misclassifying known inputs: They can be intentional attacks or natural consequences of the environment.
Figure 11. Adversarial Examples: Attacks and Defenses for Deep Learning.
Figure 12. Robust Physical-World Attack on Deep Learning Visual Classification (example).
Class novelty: classes of unseen objects during the ML model building: DNN can be exposed to new and relevant objects for its domain, for example, an emergency braking system for an unexpected class object.
Figure 13. Compositional Falsification of Cyber-Physical Systems with Machine Learning Components.
How to Overcome these Challenges?
A fault tolerance mechanism, such as a safety monitor (SM), should be applied to guarantee the property correctness of these systems by performing detection and mitigation actions. However, detecting, and mitigating an ML threat are two huge and different types of research. It involves explainable AI (XAI), ML, statistics, safety science, and software engineering. Therefore, how can we assure that the DNN is giving the right decision at runtime? In such critical domains, the ground truth is not known. This challenge subject is part of my Ph.D. thesis and I intend to write a post about the idea in the future.
Conclusion
The world is nonlinear. Real problems tend to be nonlinear, so their data as well. Machine learning, deep learning, and other fields try to extract patterns from it. However, despite the huge advancements, these technologies still have a lot of drawbacks. But it’s not the end for applying ML to such systems but just the beginning. Recent advances in the field propose that some drawbacks are not bugs but features. I believe that sometimes a “problem” is just something that we do not understand and not necessarily something that makes something infeasible. Perhaps, these problems are nonlinear connected. For example:
A known class with different characteristics (Distributional Shifted data) results in a novel class, and it can be sometimes just noisy data, and too much noise generates anomalies. Moreover, all of these highlighted threats can be seen as adversarial examples depending on the context, including known classes when interacting with the environment. Since several problems have boundaries between them, then maybe understanding these connections could lead us to new solutions. How to do it? Again, this is another post for the future.
About the Author: Raul Sena Ferreira
Raul Sena Ferreira is an early stage researcher for the ETN-SAS ESR1 project. His research is about computer science and artificial intelligence techniques to ensure the safety decisions of AI-based autonomous vehicles. This research is conducted at LAAS-CNRS, France.
